Tricocycloids and lax tricocycloids in a monoidal category
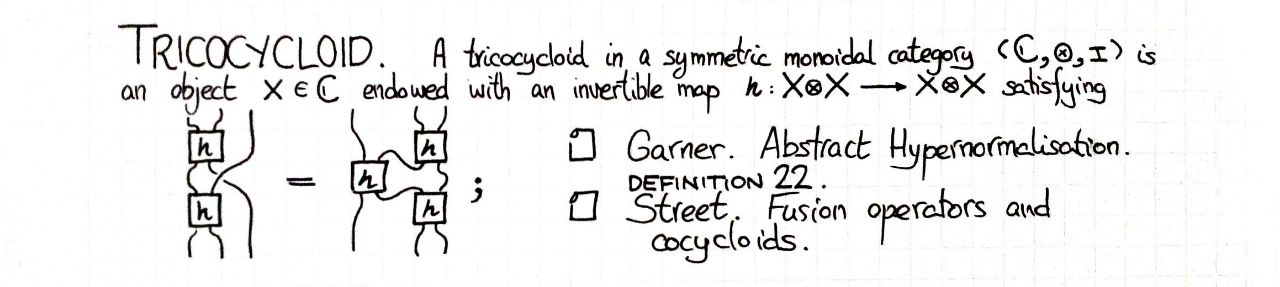

A lax tricocycloid is the non-invertible version. The following is the definition in the Set, the category of functions.
- Generalization: tricocyloid in a physical duoidal category
- Example: guards form a tricocycloid (see algebra of a symmetric tricocycloid).
- Example: every bialgebra induces a lax tricocycloid from a bialgebra.
- Example: every Hopf algebra induces a tricocycloid.
- Remark: lax tricocycloids do not rewrite easily, Knuth-Bendix completion is unilluminating.
- Construction: Lawvere theory induced by a tricocycloid.
- Construction: distributive laws from tricocycloids.
Symmetric tricocycloids
A symmetric tricocycloid has an extra endomorphism that behaves like a negation.
- Example: interval symmetric tricocycloid.
- Definition: algebra of a symmetric tricocycloid.
- Construction: Lawvere theory induced by a tricocycloid.
- Construction: distributive laws from tricocycloids.