A duoid is a duoid in the braided monoidal bicategory of posets with the product; this is in the same sense that a monoid is a monoid in the monoidal category of sets with the product.
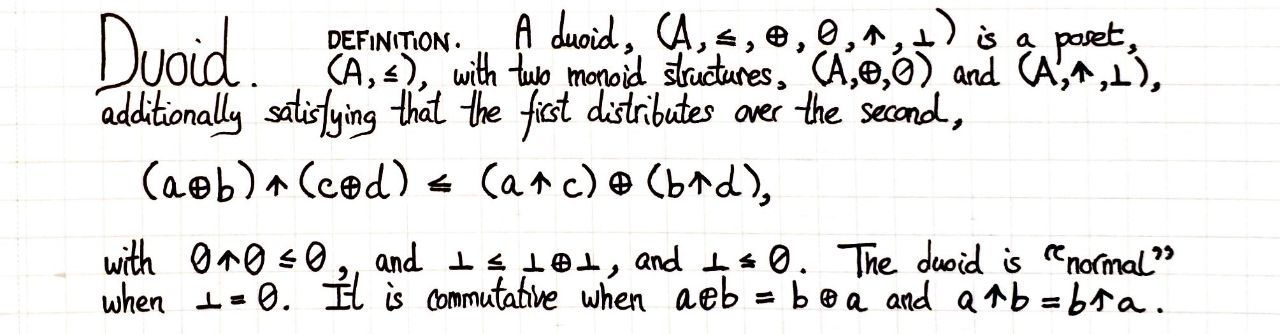
I used to call these lax duoid, to signal that they are not merely commutative monoids.

See: Poset, duoidale, Free posetal duoidale, duoidal category, Eckmann-Hilton argument.